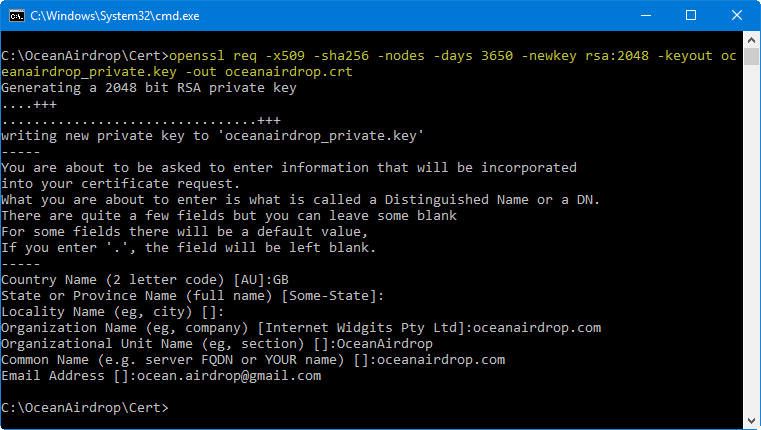
There are many reasons to self-sign SSL certificates,but I find them particularly useful for staging sites and in the early stages of a project.
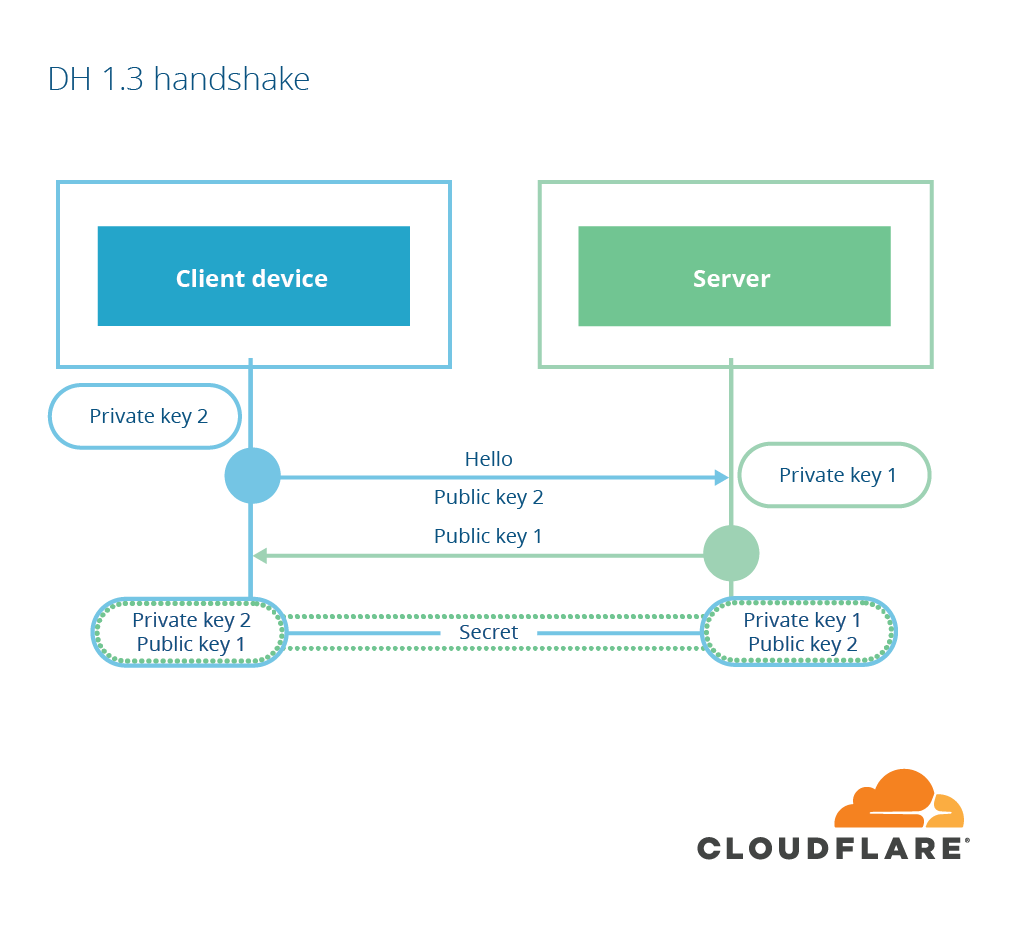
The order of the base point of Curve25519 is the a 253-bit integer 2 252 + 83648493. Choosing as private key a random positive integer less than said order is a common choice in cryptosystems based on the difficulty of the Discrete Logarithm in some group. That might be why private keys are said to be 253-bit. X25519 provides a very simple, constant time, and fast variable-base scalar multiplication algorithms. This is very good for ECDH and this is why it is used specifically for ECDH. Ed25519 instead provides a very fast fixed-base and double-base scalar multiplications, thanks to the fast and complete twisted Edwards addition law. // X25519 is the Diffie-Hellman primitive built from curve25519. DESCRIPTION The X25519, X448, ED25519 and ED448 keytypes are implemented in OpenSSL's default and FIPS providers. These implementations support the associated key, containing the public key pub and the private key priv. In the FIPS provider they are non-approved algorithms and do not have the 'fips=yes' property set. I need to implement ecdh with 25519 using openssl. Using: key = ECKEYnewbycurvename(NIDX25519) fails. Using this: EVPPKEY.pkey = NULL; EVPPKEYCTX.pctx = EVPPKEYCTXnewid(NIDX25.

I have a three command guide to self-signing an SSL certificateif you aren't interested in ECC.
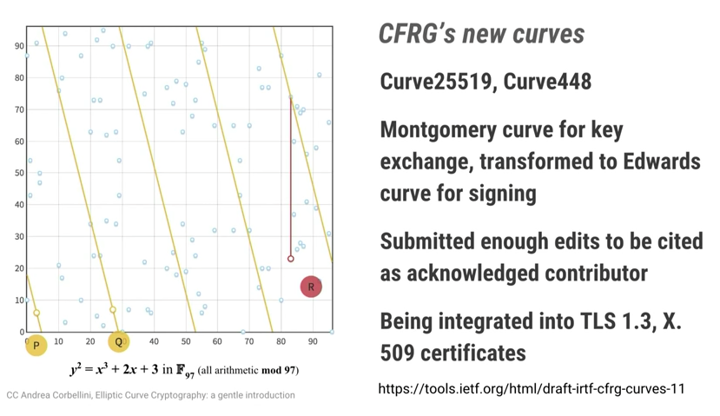
If you are interested in ECC,you may know that the main reason for using elliptic curves as the basis for communication over SSL is the small key size –where regular DSA would require 1024 bits, ECDSA (the elliptic-curve variant of DSA) would require about 160 bits.The computational power required for communication over ECDSA is also less.
This is only likely to matter in embedded systems or other highly-constrained environments.
If you are considering specifically using an ECDSA certificate like the one generated here with OpenSSL,it is probably worth reading a more detailed description by Bruce Schneier.
If you are sure you want an ECC-based certificate,doing so is just as easy as any other self-signed certificate with OpenSSL,provided that your version supports ECDSA.The commands below have been verified to work on OSX 10.8.
OpenSSL commands
The first command is the only one specific to elliptic curves.It generates a private key using a standard elliptic curve over a 256 bit prime field.You can list all available curves using
or you can use prime256v1 as I did.
The second command generates a Certificate Signing Requestand the third generates a self-signed x509 certificate suitable for use on web servers.
The check at the end ensures you will be able to use your certificate beyond 2016. OpenSSL on OS X is currently insufficient, and will silently generate a SHA-1 certificate that will be rejected by browsers in 2017. Update using your package manager, or with Homebrew on a Mac and start the process over.
More on ECC
If you're interested in elliptic curve cryptography,Wikipedia has a good introduction that includes the math behind it,as well as more specific information on ECDSA in particular.As usual, there are good links from there to learn more.
NAME
EVP_PKEY-X25519, EVP_PKEY-X448, EVP_PKEY-ED25519, EVP_PKEY-ED448, EVP_KEYMGMT-X25519, EVP_KEYMGMT-X448, EVP_KEYMGMT-ED25519, EVP_KEYMGMT-ED448 - EVP_PKEY X25519, X448, ED25519 and ED448 keytype and algorithm support
DESCRIPTION
The X25519, X448, ED25519 and ED448 keytypes are implemented in OpenSSL's default and FIPS providers. These implementations support the associated key, containing the public key pub and the private key priv.
In the FIPS provider they are non-approved algorithms and do not have the 'fips=yes' property set. No additional parameters can be set during key generation.
Common X25519, X448, ED25519 and ED448 parameters
In addition to the common parameters that all keytypes should support (see 'Common parameters' in provider-keymgmt(7)), the implementation of these keytypes support the following.
This is only supported by X25519 and X448. The group name must be 'x25519' or 'x448' respectively for those algorithms. This is only present for consistency with other key exchange algorithms and is typically not needed.
The public key value.

The private key value.
Used for getting and setting the encoding of a public key for the X25519 and X448 key types. Public keys are expected be encoded in a format as defined by RFC7748.
ED25519 and ED448 parameters
There are many reasons to self-sign SSL certificates,but I find them particularly useful for staging sites and in the early stages of a project.
The order of the base point of Curve25519 is the a 253-bit integer 2 252 + 83648493. Choosing as private key a random positive integer less than said order is a common choice in cryptosystems based on the difficulty of the Discrete Logarithm in some group. That might be why private keys are said to be 253-bit. X25519 provides a very simple, constant time, and fast variable-base scalar multiplication algorithms. This is very good for ECDH and this is why it is used specifically for ECDH. Ed25519 instead provides a very fast fixed-base and double-base scalar multiplications, thanks to the fast and complete twisted Edwards addition law. // X25519 is the Diffie-Hellman primitive built from curve25519. DESCRIPTION The X25519, X448, ED25519 and ED448 keytypes are implemented in OpenSSL's default and FIPS providers. These implementations support the associated key, containing the public key pub and the private key priv. In the FIPS provider they are non-approved algorithms and do not have the 'fips=yes' property set. I need to implement ecdh with 25519 using openssl. Using: key = ECKEYnewbycurvename(NIDX25519) fails. Using this: EVPPKEY.pkey = NULL; EVPPKEYCTX.pctx = EVPPKEYCTXnewid(NIDX25.
I have a three command guide to self-signing an SSL certificateif you aren't interested in ECC.
If you are interested in ECC,you may know that the main reason for using elliptic curves as the basis for communication over SSL is the small key size –where regular DSA would require 1024 bits, ECDSA (the elliptic-curve variant of DSA) would require about 160 bits.The computational power required for communication over ECDSA is also less.
This is only likely to matter in embedded systems or other highly-constrained environments.
If you are considering specifically using an ECDSA certificate like the one generated here with OpenSSL,it is probably worth reading a more detailed description by Bruce Schneier.
If you are sure you want an ECC-based certificate,doing so is just as easy as any other self-signed certificate with OpenSSL,provided that your version supports ECDSA.The commands below have been verified to work on OSX 10.8.
OpenSSL commands
The first command is the only one specific to elliptic curves.It generates a private key using a standard elliptic curve over a 256 bit prime field.You can list all available curves using
or you can use prime256v1 as I did.
The second command generates a Certificate Signing Requestand the third generates a self-signed x509 certificate suitable for use on web servers.
The check at the end ensures you will be able to use your certificate beyond 2016. OpenSSL on OS X is currently insufficient, and will silently generate a SHA-1 certificate that will be rejected by browsers in 2017. Update using your package manager, or with Homebrew on a Mac and start the process over.
More on ECC
If you're interested in elliptic curve cryptography,Wikipedia has a good introduction that includes the math behind it,as well as more specific information on ECDSA in particular.As usual, there are good links from there to learn more.
NAME
EVP_PKEY-X25519, EVP_PKEY-X448, EVP_PKEY-ED25519, EVP_PKEY-ED448, EVP_KEYMGMT-X25519, EVP_KEYMGMT-X448, EVP_KEYMGMT-ED25519, EVP_KEYMGMT-ED448 - EVP_PKEY X25519, X448, ED25519 and ED448 keytype and algorithm support
DESCRIPTION
The X25519, X448, ED25519 and ED448 keytypes are implemented in OpenSSL's default and FIPS providers. These implementations support the associated key, containing the public key pub and the private key priv.
In the FIPS provider they are non-approved algorithms and do not have the 'fips=yes' property set. No additional parameters can be set during key generation.
Common X25519, X448, ED25519 and ED448 parameters
In addition to the common parameters that all keytypes should support (see 'Common parameters' in provider-keymgmt(7)), the implementation of these keytypes support the following.
This is only supported by X25519 and X448. The group name must be 'x25519' or 'x448' respectively for those algorithms. This is only present for consistency with other key exchange algorithms and is typically not needed.
The public key value.
The private key value.
Used for getting and setting the encoding of a public key for the X25519 and X448 key types. Public keys are expected be encoded in a format as defined by RFC7748.
ED25519 and ED448 parameters
The empty string, signifying that no digest may be specified.
CONFORMING TO
- RFC 8032
- RFC 8410
EXAMPLES
An EVP_PKEY context can be obtained by calling:
An X25519 key can be generated like this:
An X448, ED25519, or ED448 key can be generated likewise.
SEE ALSO
EVP_KEYMGMT(3), EVP_PKEY(3), provider-keymgmt(7), EVP_KEYEXCH-X25519(7), EVP_KEYEXCH-X448(7), EVP_SIGNATURE-ED25519(7), EVP_SIGNATURE-ED448(7)
COPYRIGHT
Openssl Examples
Copyright 2020 The OpenSSL Project Authors. All Rights Reserved.
How To Use Openssl
Licensed under the Apache License 2.0 (the 'License'). You may not use this file except in compliance with the License. You can obtain a copy in the file LICENSE in the source distribution or at https://www.openssl.org/source/license.html.

